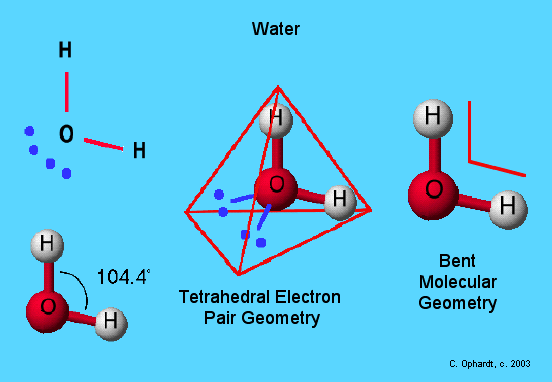
In a previous post I discussed bond hybridisation theory in the context of the Methane molecule.
Now we come to examine how the model is used to both describe and predict the properties we observe about the ethene molecule.
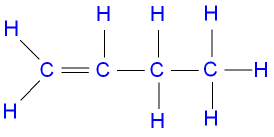
Here is a displayed formula of ethene showing the bond angles and bond lengths:
Ethene has a trigonal planar shape about each carbon atom i.e. it is a flat molecule.
Lets look closely at ethene.
What stands out is the double bond and the knowledge that one bond is weaker than the other.
We know this from studies of the reactions of ethene.
Addition reactions involve the addition of a molecule across the double bond in which the weaker one of the two bonds breaks.
I have blogged on this phenomenon here.
Ethene has three equivalent covalent bonds around each carbon atom and the additional weaker bond between the two carbon atoms.
It has been calculated and shown experimentally that a mole of the C-H bonds takes about 416 kJ to break.
A mole of the C=C bonds takes around 614kJ and a C-C bond 347kJ leaving 267kJ to fit the other bond in the double bond.
How can we explain this data?
When we examine the electron arrangement of carbon we find this:
The lowest energy carbon atom has its 6 electrons in the following configuration:
Carbon 1s2 2s2 2p2
The four electrons in the second energy level are in two sub shells of slightly different energy.
Now there's the issue.
For these four electrons to remain in these two subshells would not make four covalent bonds with hydrogen electrons around the carbon atom.
To arrive at three equivalent bonds, plus the weaker one we observe in ethene, the hybridisation model suggests the promotion of one electron into the empty p orbital.
But then - and this is new in ethene - hybrid orbitals form from two p orbitals and an s orbital.
This model is illustrated below.
In this model an electron is promoted to the empty 2pz orbital and then the 2s and two 2p orbitals "hydridise" to form three equal energy atomic orbitals in the carbon outer shell.
These three atomic orbitals are designated sp2 because each one is formed from an s orbital and two p orbitals.
That leaves an electron in a 2p orbital - in the example above it is in the 2pz orbital.
When it comes to bonding with hydrogen, the model suggests that the two hydrogen atoms overlap their 1s atomic orbitals with two of the sp2 orbitals of carbon.
That gives us two C-H σ bonds.
The other sp2 orbital overlaps with that of the other carbon atom, again giving a σ bond, only this time joining two carbon atoms together.
Question is what does the model suggest gives rise to the other bond of the double bond?
Here we have a very new and original suggestion.
And it is a model that fits the reality of ethene.
Ethene has another property we've not yet mentioned.
This property is that the double bond cannot rotate freely, its rotation is severly restricted.
We know this from the existence of E-Z or cis - trans isomers.
The hybridisation model suggests that another kind of bond forms between the two carbon atoms that stops rotation.
It is called a π bond and it is formed from the side ways overlap of the two remaining 2pz atomic orbitals.
So a spatial representation of the atoms in ethene looks like this:
Now the strange thing is that the π bond is both the blue and red parts shown in the diagram.
Both spaces have a probability of finding the electron of about 95%.
The two comprise the whole bonding molecular orbital (MO).
This diagram shows us a model of the ethene molecule that is the right shape with the right bond angles between the two C-H bonds at either end of the molecule .
In the model, molecular orbitals (MO) result from the overlap of atomic orbitals.
VSEPR theory is supported on this hybridisation model because there is a higher electron density between the carbon atoms due to the π bond.
This higher electron density means that the two C-H sigma bonds at each end of the molecule will be pushed closer together than in a normal trigonal planar molecule.
We ought to see the H-C-H angle drop below 120º and we do: it is 117.4º.
New Pages on the "Mole" and "Using the Mole" in chemical calculations are here
Now we come to examine how the model is used to both describe and predict the properties we observe about the ethene molecule.
Here is a displayed formula of ethene showing the bond angles and bond lengths:
Ethene has a trigonal planar shape about each carbon atom i.e. it is a flat molecule.
Lets look closely at ethene.
What stands out is the double bond and the knowledge that one bond is weaker than the other.
We know this from studies of the reactions of ethene.
Addition reactions involve the addition of a molecule across the double bond in which the weaker one of the two bonds breaks.
I have blogged on this phenomenon here.
Ethene has three equivalent covalent bonds around each carbon atom and the additional weaker bond between the two carbon atoms.
It has been calculated and shown experimentally that a mole of the C-H bonds takes about 416 kJ to break.
A mole of the C=C bonds takes around 614kJ and a C-C bond 347kJ leaving 267kJ to fit the other bond in the double bond.
How can we explain this data?
When we examine the electron arrangement of carbon we find this:
The lowest energy carbon atom has its 6 electrons in the following configuration:
Carbon 1s2 2s2 2p2
The four electrons in the second energy level are in two sub shells of slightly different energy.
Now there's the issue.
For these four electrons to remain in these two subshells would not make four covalent bonds with hydrogen electrons around the carbon atom.
To arrive at three equivalent bonds, plus the weaker one we observe in ethene, the hybridisation model suggests the promotion of one electron into the empty p orbital.
But then - and this is new in ethene - hybrid orbitals form from two p orbitals and an s orbital.
This model is illustrated below.
In this model an electron is promoted to the empty 2pz orbital and then the 2s and two 2p orbitals "hydridise" to form three equal energy atomic orbitals in the carbon outer shell.
These three atomic orbitals are designated sp2 because each one is formed from an s orbital and two p orbitals.
That leaves an electron in a 2p orbital - in the example above it is in the 2pz orbital.
When it comes to bonding with hydrogen, the model suggests that the two hydrogen atoms overlap their 1s atomic orbitals with two of the sp2 orbitals of carbon.
That gives us two C-H σ bonds.
The other sp2 orbital overlaps with that of the other carbon atom, again giving a σ bond, only this time joining two carbon atoms together.
Question is what does the model suggest gives rise to the other bond of the double bond?
Here we have a very new and original suggestion.
And it is a model that fits the reality of ethene.
Ethene has another property we've not yet mentioned.
This property is that the double bond cannot rotate freely, its rotation is severly restricted.
We know this from the existence of E-Z or cis - trans isomers.
The hybridisation model suggests that another kind of bond forms between the two carbon atoms that stops rotation.
It is called a π bond and it is formed from the side ways overlap of the two remaining 2pz atomic orbitals.
So a spatial representation of the atoms in ethene looks like this:
Now the strange thing is that the π bond is both the blue and red parts shown in the diagram.
Both spaces have a probability of finding the electron of about 95%.
The two comprise the whole bonding molecular orbital (MO).
This diagram shows us a model of the ethene molecule that is the right shape with the right bond angles between the two C-H bonds at either end of the molecule .
In the model, molecular orbitals (MO) result from the overlap of atomic orbitals.
VSEPR theory is supported on this hybridisation model because there is a higher electron density between the carbon atoms due to the π bond.
This higher electron density means that the two C-H sigma bonds at each end of the molecule will be pushed closer together than in a normal trigonal planar molecule.
We ought to see the H-C-H angle drop below 120º and we do: it is 117.4º.
New Pages on the "Mole" and "Using the Mole" in chemical calculations are here