Spectroscopic Techniques (1) Nuclear Magnetic Resonance Spectroscopy (NMR)

NMR spectroscopy is one of the most versatile and valuable non-invasive investigative techniques chemists have these days to identify and put together the structures of molecules.

How does it work?

This is not an easy explanation for school and college students to get a hold of.

I’m just going to discuss ¹H proton nmr spectroscopy but if you delve deeper into this topic you will come across equally valuable ¹³C and ³¹P nmr as well.

You'll notice that these species all have an odd number of nucleons.

So if the proton is Deuterium with two nucleons this does not register in nmr.

Background NMR theory

Proton nmr tells us about the chemical environment of ¹H hydrogen nuclei in molecules.

¹H hydrogen nuclei spin about an axis.

They have spin quantum number ½

As they spin, the positive charge moves and creates its own very small magnetic field. 

Put this spinning ¹H hydrogen nucleus in an external magnetic field and it will either spin so as to line itself up with this external magnetic field or it will spin against the field. 

What happens is like what happens when you put a compass needle in the Earth’s magnetic field and the needle lines up with it pointing north. 

Now back to the proton, if the nucleus is lined up with the external field it has quantum number  + ½ . 

But if the spinning nucleus is aligned against the external field it has quantum number – ½ .

In fact, most nuclei line up with the field and far fewer line up against it. 

What this means is that there is an energy gap, ∆E, between the two states of the spinning nucleus. 

 

 

Radiation of the right frequency (low frequency radio waves) will match ∆E and lift some nuclei from spin state + ½   to spin state – ½: this is said to ‘flip’ the nuclei.

Energy is released (it's called relaxation) to the surroundings or other nuclei as the nuclei return to their original ground state. 

This energy registers as an nmr pulse in the nmr spectrum.  

What happens in an actual molecule to the ¹H protons if placed in an external magnetic field?

In an external magnetic field, the electrons around each ¹H nucleus in the molecule move and flow to produce a local, very small magnetic field that opposes the applied field. 

This means that all the ¹H nuclei in the molecule feel a magnetic field slightly smaller than the one applied to the molecule.

Each ¹H nucleus is then in a different magnetic environment according to the number and position of the electrons around it. 

These very slight differences in magnetic field show up in the nmr spectrum as the nuclei flip and relax.

These differences are very small for ¹H nuclei — in parts per million (ppm) of magnetic field density B.

However, it is possible to measure these so-called chemical shifts ∂.

The chemical shift ∂ value gives a sense of how much the electrons around the ¹H proton have “shielded” it from the full effect of the applied external magnetic field.

The more shielding, the larger the chemical shift ∂ value and the lower ∆E. 

The chemical shift ∂ values need a reference point. 

The magnetic signal from Tetra Methyl Silane TMS (CH₃)₄Si is used as a reference as its protons are hardly shielded from the effect of the external magnetic field. 

tetramethylsilane

All other magnetic signals of chemical shift ∂ are the result of the electrons in the molecule shielding that particular ¹H proton more or less.

You can see here the effect of the π system of electrons above and below the carbon ring.

Table of chemical shifts are available on the internet.

Equally, if there is a very electronegative atom in a molecule its electrons will also shield any ¹H protons and these protons will resonate at higher chemical shift ∂ values. 

C¹H—R                         C¹H—Cl

∂  1.5                               ∂  4.2

Spin–spin coupling

Another thing can happen if there are hydrogen atoms on different carbon atoms next to each other in the molecule. 

The signal from one ¹H proton will split the signal from the other proton and vice versa. 

Usually, the effect just happens over a distance of one C–C bond.

The effect is called spin–spin coupling.

To predict how the signal from the one proton will split the signal from the other you have to count the number of protons on the adjacent carbon atom. 

In simple cases a single signal will split (n+1) times where n is the number of ¹H hydrogen atoms on the adjacent carbon atom. 

For example:  Ethanol  CH₃CH₂OH

The signal from the hydrogen atoms on the –CH₂ – group will split the signal from the CH₃ – group because it will interact with the magnetic field produced by the CH₃ – group.

If we use the (n+1) rule then n for the CH₂ group is 2+1 =3 so that the signal from the CH₃ group will be split into a triplet.

Conversely, the –CH₃– group (n+1 or 3+1=4) will split the signal from the –CH₂ – group into a quartet.

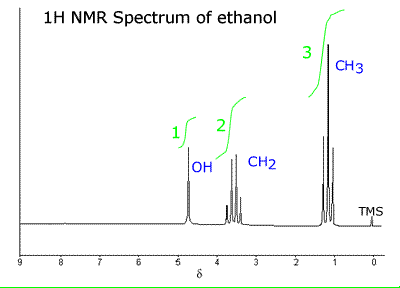
Here then is the nmr spectrum of ethanol:

You can see several things here.

First, the –O–H group is a singlet because the oxygen decouples the hydrogen from the others in the molecule so there is no spin–spin coupling effect/no peak splitting. 

Second, the chemical shift ∂ for the –O–H hydrogen is shifted to 4.7 because of the electrons on the electronegative oxygen atom. 

Third, the CH₂ is a quartet as we predicted.

Fourth, the CH₃ is a triplet as we predicted.

Fifth, the peak areas (given in green) show us that they are in the ratio of the number of hydrogen atoms on each carbon. 

Sixth, the intensity of the peaks take up the pattern of Pascal’s triangle. 

Seventh, if the molecule were CH₃CH₂OD there would be no singlet because of the deuterium atom.  

At school and college level probably the most complex molecule you will have to deal with is something like butanone or ethyl ethanoate. 

Here are examples of both nmr spectra below:

Butanone

Ethyl acetate

Some important chemical shifts:

OH in alcohols ∂ between 2 and 4

OH in carboxylic acids ∂ between 10 and 12

Alkane CH between ∂ 0.25 and 1.75 but note: CH > CH₂ > CH₃

O–CH in alcohols ∂ between 3 and 4

Halogen –CH in halogenoalkanes  ∂ between 2.2 and 4.2

Beware symmetrical molecules such as  CH₂OH CH₂OH which has only two peaks and (CH₃)4C which has just one peak (like TMS)


You’ll also find many examples of spectra if you click here.

Some important chemical shifts

Reaction Kinetics (6) How Temperature affects Reaction Rate

In this blog I’m going to introduce you to the mathematical model that shows how temperature affects reaction rate.

You probably learned from your earliest days in chemistry that temperature affects reaction rate

Many young students think that if they heat a reaction in a test-tube more/hotter the reaction will go faster.

These young students aren’t sure why the reaction should go faster they seem just intuitively to know that the reaction will go faster.

And for the most part reactions do go faster at higher temperatures.

So what might be going on in the reaction mix?

Collision Theory

That brings us to think about collision theory.

Can a reaction between substances take place without their particles “colliding”?

The answer is no, in collision theory the fundamental assumption about chemical change is that it takes place between two, not necessarily different, particles colliding.

Each collision is also assumed to be between just two particles because the chances of three colliding at the same time are very remote. 

The only other way a reaction might start is for one particle to split into two. 

Collision theory also suggests that not all collisions are effective at bringing about chemical change.

Think about collisions between vehicles on the road.

Vehicles can collide head–on or they can collide sideways, one car hitting the side of the other or they can just make glancing blows with very little if any damage or even a head on collision can cause no damage if it is at a very slow speed. 

Transfer those ideas to particles in a chemical reaction and you see that the biggest assumptions in collision theory are that effective collisions

a) occur when particles have sufficient energy to collide and break bonds: the activation energy

b) have to have the particles in the correct orientation to each other in space.

There is then an energy barrier to effective collision between particles and therefore to reaction taking place.

This energy barrier to reaction is called the Activation Energy E_A

This chart shows how activation energy can be a barrier to reaction.

So how many particles in a reaction mix actually have the activation energy?

This chart shows how gas molecules are distributed over different kinetic energies at two temperatures: T₁ K and a hotter temperature T₂ K.

What does this chart tell us?

First, the area under each curve is the same because it represents the number of gas molecules in the reaction mixture.

This number does not change as the temperature rises.

Second, as the temperature of the gas rises more molecules occupy higher energy states so the most occupied value (the peak of each curve) drops and moves right to a higher energy value.  

Third, two activation energies are marked on the graph. E_a1 and E_a2.  What you notice is that at the higher temperature there are more molecules at or above the activation energy. 

So at higher temperatures reactions tend to go faster because there are more particles that possess an energy at or greater than the activation energy.

The chart below summarises these points

Arrhenius suggested that the effect of temperature on the rate of a reaction depended on the activation energy of the reaction in this mathematical relationship:

k  =    A e ^–Ea/RT

where

k       the rate constant

A       a factor associated with the orientation of the particles on reaction and their collision frequency

E_a      the activation energy (J.mol^-1)

R       the universal gas constant (8.314 J.mol^-1.K^-1)

T       the temperature of the reaction (K)

Taking natural logs of this relationship yields a relationship in the form of y = mx + c thus:

ln k  =  ln A  –  E_a/RT

so that a plot of ln k vs 1/T yields a straight line with gradient  –E_a/R and an intercept corresponding to ln A.

Here are the results from an experiment to determine the activation energy for the iodination of propanone.

How do we calculate the activation energy?

First, the temperatures for each experiment have been converted in to Kelvin by adding 273.

Second, the inverse of these Kelvin temperatures have been calculated.

Third, the natural log of the rate data has been determined using the spreadsheet ‘ln’ function.

Fourth, it then becomes relatively simple to produce an x-y scatter plot of the ln(rate) data vs 1/T.

Fifth, adding the trendline and its equation gives the gradient of the line from which the activation energy can be calculated as follows:

Gradient is   –6458  =  –E_a/R

Therefore:  E_a   =   6458  ×  8.314 J.mol^–1

                           =  53.7 kJ.mol^–1

I’ve added below the script for an experiment in which you can determine the activation energy for the bromate/bromide reaction. 

You can try this out in the lab it’s different because it uses phenol and  methyl red and is a clock reaction. 

See what you think.

Investigating the effect of temperature on the rate of reaction between bromide and bromate ions. 

Introduction

The reaction to be studied in this experiment is between bromate(V) and bromide ions in the presence of acid and occurs according to the equation:

KBrO₃  + 5KBr  +  3H₂SO₄     =         3K₂SO₄  +  3H₂O   + 3Br₂  [1]

In this reaction, the potassium and sulphate ions are “spectator” ions in that they are not themselves materially affected, so, in ionic terms the reaction may be summarised as,

BrO₃^-    +   5Br^-   +    6H⁺   =    3Br₂   +     3H₂O   [2]

The rate of this reaction can be conveniently measured by measuring the rate at which bromine is produced.

To do this, a limited amount of phenol and the dye methyl red are added to the reaction mixture, the bromine reacts very rapidly with the phenol to form 2,4,6–tribromophenol.

Once all the phenol added has reacted there will be excess Br₂ released by the reaction.

This will oxidise the methyl red causing the disappearance of the red colour in the reaction mixture.

Thus, if the time (t) taken for the red colour to disappear is measured from the start of the reaction then this will closely correspond to the time taken for the reaction to produce enough bromine to react with a known quantity of phenol.

Provided the concentrations of the reactants are set at particular values then the rate of reaction will depend only on temperature. 

Also, if the quantity of phenol added is kept the same, the value of the rate constant at a given temperature will be proportional to t^-1. 

Thus by measuring t at various temperatures we can calculate a value for the activation energy (E_a) for the reaction. (see Equation 4 in the theory section).

Experimental Procedure

1.   Pipette 10cm³ of the bromate(V)–bromide solution provided in the laboratory and 10 cm³ of phenol solution into a 100ml conical flask. 

2.   Place the flask in a large plastic trough of water at the temperature (T) at which the reaction is to be run. (N.B. Place a thermometer in the flask to determine as accurately as possible the actual reaction temperature. Ensure that the thermometer bulb is covered by the solution).

3.   Pipette 25 cm³ of 0.5M sulphuric acid into another 100ml conical flask, add 10drops methyl red solution and stand the flask in the water bath/trough.

4.   When the solutions have reached the same steady temperature, add the sulphuric acid/methyl red mix to the bromate(V)-bromide/phenol mixture and start the stop clock.

5.   Take the reaction mixture out of the water-bath/trough, stand the flask on a white tile next to a reference flask containing water and shake gently from time to time until the red coloration disappears.

6.   Note the time (t) for this to occur and the final temperature of the solution.

The procedure described above should be repeated at four different temperatures in the range 0^oC to 65^oC, the reaction temperature and time taken for the colour change to occur in the methyl red being carefully noted in each case.

Theory

If a chemical reaction is to take place between two reactive species, these species must collide with each other in order that bond breaking and/or making can lead to the formation of products.

In gas phase reactions, collisions between molecules are easily envisaged. 

In solution the reactive species are less free to move about, being hindered by solvent molecules. 

However, whether in the gas phase or solution it is clear that not every collision is successful in bringing about reaction.

For example, in a gas at one atmosphere pressure and at room temperature there are typically 10²⁸ collisions per cubic centimeter per second.

Therefore, if all collisions were successful all gas phase reactions would be over in about 10^-9 seconds, which clearly does not happen.

Therefore there must be some other factor that operates to reduce the effectiveness of collisions in bringing about reaction.  

In order for a reaction to occur, it is not sufficient that molecules simply collide, they must do so with enough energy.

The numerical value of the minimum energy is called the ACTIVATION ENERGY (Ea) and is specific to a particular reaction.

In this experiment, you will calculate the activation energy for the bromate(V)-bromide reaction.

The rates of most reactions are known to increase significantly with rising temperature. 

A good rule of thumb is that the rate roughly doubles for every 10^oC rise.

There are exceptions to this but on the whole it is a fair guide.

In 1889 Arrhenius proposed that the temperature dependence of the rate of reaction is governed by the equation that now bears his name,

k = A exp [-Ea/RT]          [3]

where k is the rate constant, Ea is the activation energy, R is the gas constant and T the temperature in degrees Kelvin. 

The pre-exponential term A is the property of the particular reaction related to the collision frequency of the reactive species.

We might thus expect A to be itself temperature dependent and this is indeed the case.

However, in equation (2), the dependence of k on temperature is dominated by the strong exponential term, so, in the analysis of experimental data, the dependence of A on temperature is usually ignored as a first approximation. 

Equation (2) can be rewritten in logarithmic form,

log₁₀k = log₁₀A – E_a/2.303R   T    [4]

[ y       = c         – m                   x ]

where R, the gas constant, is 8.314 J.mol^-1K^-1

A graph of log₁₀k against 1/T is therefore expected to be linear with negative slope given by –Ea/2.303R. 

Measurement of a reaction rate at various temperatures therefore provides us with a means of determining the activation energy for the reaction.

Questions

1.   Complete this table of the results of your experiments:

Expt	Temp /oC	Temp (T) /K	1/T /K-1	Time (t) /s	1/t /s-1	log10(1/t)	2.303 log10(1/t)
1.
2.
3.
4.
5.
6.

2.  Plot a graph of 2.303 log₁₀k vs 1/T and determine from the slope the activation energy of the reaction. 

3.  Draw an energy profile of the reaction between bromate(V) and bromide ions marking on your profile the enthalpy change of the reaction (∆H) and the activation energy E_a.

4.  Leave your final reaction mixture to stand and note down and explain any changes you observe after 10-15 mins.